Qual è il miglior costruttore che conoscete?
Vi passeranno per la mente un sacco di nomi di architetti, ingegneri più o meno famosi, imprese o ditte di livello nazionale o internazionale....niente di tutto ciò!
La risposta è che la natura è la miglior costruttrice...fa e disfa secondo criteri di efficienza ed efficacia che l'uomo non ha mai saputo fare!
Guardate questo video ispirato ai numeri, alla geometria ed alla natura!
Qui di seguito ci sarà una spiegazione del video appena visto.
L'animazione comincia presentando una serie di numeri. E' una sequenza molto famosa e riconosciuta molti secoli fa a Leonardo di Pisa, un matematico italiano del tredicesimo secolo, denominato anche Fibonacci. Questa è proprio la sequenza del Fibonacci, già comunque nota ancora prima ai matematici indiani.
Ciò è una sequenza infinita di numeri naturali dove il primo valore è 0, il seguente è 1 e, da lì, ogni importo è ottenuto aggiungendo i due precedenti.
I valori di questa sequenza compaiono in numerose applicazioni come nella spirale del Fibonacci, che è stata usata sempre come approssimazione alla spirale aurea (un tipo di spirale logaritmica) perché più facile da rappresentare (vedi processo di costruzione nel video).
Si generano in primo luogo quadrati che corrispondono ad ogni valore sulla sequenza: 1x1 - 1x1 - 2x2 - 3x3 - 5x5 - 8x8, ecc. e sono organizzati come nella figura a sinistra.
Poi si disegna un quarto di circonferenza (con angolo di 90°) all'interno di ogni piccolo quadrato e si può notare come si sviluppa per gradi la spirale del Fibonacci (grafico a destra).
In questa figura è stata introdotta una correzione ottica per ottenere delle curve simili a quelle della vera spirale dorata (più armoniosa ed equilibrata).
Mentre si guarda l'animazione si ha l'idea che la spirale del Fibonacci (o la spirale aurea, indiferentemente) è all'origine della figura di un Nautilus; questo non è del tutto esatto. L'autore del video ha trovato una ricerca dove si dimostra la non corrispondenza tra la spirale ed il Nautilus dopo aver già pubblicato il montaggio.
La seconda parte dell'animazione introduce il concetto del rapporto aureo attraverso la costruzione di un rettangolo aureo partendo da un semplice quadrato.
Questo rettangolo era già conosciuto in periodi antichi come rapporto aureo o proporzione divina: il rapporto dato dalla somma dei valori (a+b) ed il valore più grande(a), è uguale al rapporto tra la quantità più grande e quella più piccola.
Può anche essere scritta sotto forma di proporzione:
(a + b) : a = a : b
Il risultato di questo rapporto è un numero irrazionale.
Non è stato concepito come unità di misura lineare ma come un semplice rapporto di proporzionalità tra due segmenti.
Si trovano molti esempi del suo utilizzo in arte ed in architettura già ai tempi dei Babilonesi, degli Assiri e dei Greci.
Nel video non è evidente il forte collegamento fra la sequenza del Fibonacci ed il rapporto aureo.
Se si divide ogni valore delle serie di Fibonacci con il precedente, il risultato tende al numero irrazionale 'Phi'. Più alto è il valore, maggior sarà l'approssimazione (essendo numero irrazionale ha decimali infiniti).
Un altro passo dell'animazione è quello che introduce il concetto di angolo aureo, il rapporto angolare fra due segmenti circolari:
Questo valore è profondamente presente in natura come i petali dei fiori, le foglie o i semi di girasole.
La natura li dispone seguendo quest'angolo per ottimizzare la superficie esposta al sole (Filotassi).
La logica di questo procedimento è illustrato nella figura sotto riportata:
Si noti il legame tra la sequenza di Fibonacci ed il rapporto aureo.
I semi sono distribuiti secondo il modello a spirale. Nell'immagine di sinistra si evidenziano tre delle spirali che potrebbero essere trovate su quasi tutto il girasole.
Per esempio quella verde compare 55 volte (numero che non a caso fa parte della sequenza di Fibonacci).
Stesso ragionamento per quella color ciano che si ripete per 34 volte e quella arancione 21.
Un altro passo dell'animazione introduce un concetto meno è conosciuto: lo schema di Voronoi (Voronoi Tesselation) o Diriclet Tessellation.
Queste forme geometriche sono basate su un modello di distribuzione che è facilmente riconoscibile in molte strutture naturali, come le ali di alcuni insetti o di queste piccole ramificazioni capillari delle foglie di una specifica pianta.
È inoltre ampiamente usato per ottimizzare i sistemi di comunicazione come installazione delle antenne del telefono.
Si hanno due punti: uno rosso e un altro azzurro. Si inizia disegnando un segmento che unisce questi puntini ed un secondo ortogonale passante per il punto di mezzeria del primo.
Si aggiunga un terzo punto verde che giace sulla retta perpendicolare e lo si unisca ai primi due punti. Si tracci anche in questo caso le perpendicolari passanti per il punto medio.
Continuando ad aggiungere punti con la stessa logica si otterrà una serie di poligoni - mattonelle di Voronoi - attorno ad un insieme di "punti di controllo". Quindi il perimetro di ciascuna mattonella è equidistante ai punti vicini e definisce la zona di influenza.
Tutti questi segmenti che collegano i punti formano una struttura triangolare denominata "triangolazione di Delaunay".
Attraverso le triangolazione di Delaunay si può controllare o modificare una struttura di questo tipo:
Se si utilizzano i centri di ogni circonferenza, contrassegnati dal colore rosso, come vertici di poligoni si ottiene la piastrellatura di Voronoi.
Se si analizzano le ali di una libellula al microscopio si troverà una somiglianza con la struttura sopra descritta, con alcune eccezioni ovviamente.
Fonte Etérea
| Non perdere il prossimo articolo: | ||
| < | ||
| Aiutaci condividendo questo artcolo: | ||

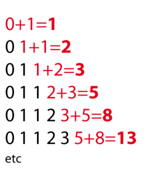







































1 commenti:
Anche se apparentemente buttato tutto li a caso, é interessantissimo vedere questi strettisimi rapporti tra matematica e natura.
La matematica è nata misurando quello che esisteva in natura ed è quindi "normale" che tutto abbia una logica ben precisa...
Posta un commento